A binary expression tree is a specific kind of a binary tree used to represent expressions
The leaves of a binary expression tree are operands, such as constants or variable names, and the other nodes contain operators. These particular trees happen to be binary, because all of the operations are binary, and although this is the simplest case, it is possible for nodes to have more than two children. It is also possible for a node to have only one child, as is the case with the unary minus operator
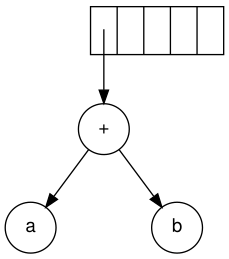
The next symbol is a '+'. It pops the two pointers to the trees, a
new tree is formed, and a pointer to it is pushed onto to the stack.
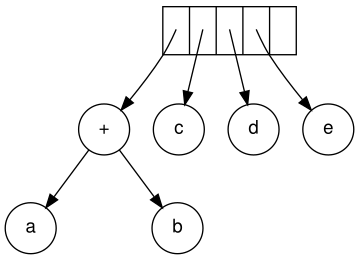
Next, c, d, and e are read. A one-node tree is created for each and a
pointer to the corresponding tree is pushed onto the stack.
Continuing, a '+' is read, and it merges the last two trees.
Now, a '*' is read. The last two tree pointers are popped and a new tree is formed with a '*' as the root.
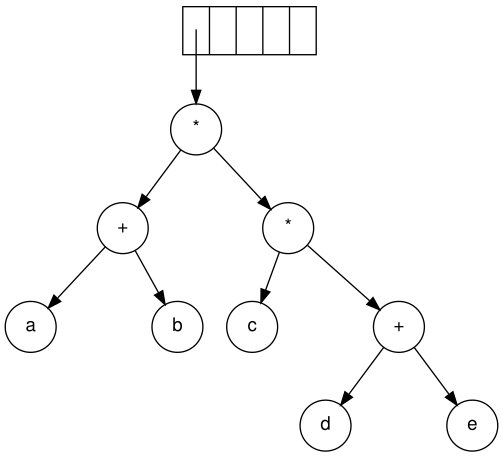
Finally, the last symbol is read. The two trees are merged and a pointer to the final tree remains on the stack.[5]
Steps to construct an expression tree a b + c d e + * *
The leaves of a binary expression tree are operands, such as constants or variable names, and the other nodes contain operators. These particular trees happen to be binary, because all of the operations are binary, and although this is the simplest case, it is possible for nodes to have more than two children. It is also possible for a node to have only one child, as is the case with the unary minus operator
Construction of an expression tree
The evaluation of the tree takes place by reading the postfix expression
one symbol at a time. If the symbol is an operand, one-node tree is
created and a pointer is pushed onto a stack. If the symbol is an operator, the pointers are popped to two trees T1 and T2 from the stack and a new tree whose root is the operator and whose left and right children point to T2 and T1 respectively is formed . A pointer to this new tree is then pushed to the Stack
Example
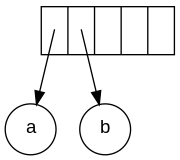
The input is: a b + c d e + * * Since the first two symbols are operands, one-node trees are created and pointers are pushed to them onto a stack. For convenience the stack will grow from left to right.
Stack growing from left to right
Formation of a new tree
Creating a one-node tree
Merging two trees
Forming a new tree with a root
Steps to construct an expression tree a b + c d e + * *