B+ Trees

Download PPT
Go to Animation

B - Trees

Download PPT
Go to Animation
Example PPT 

In a binary search tree, AVL Tree, Red-Black tree etc., every node can have only one value (key) and maximum of two children but there is another type of search tree called B-Tree in which a node can store more than one value (key) and it can have more than two children. B-Tree was developed in the year of 1972 by Bayer and McCreight with the name Height Balanced m-way Search Tree. Later it was named as B-Tree.

B-Tree can be defined as follows...

B-Tree is a self-balanced search tree with multiple keys in every node and more than two children for every node.

Here, number of keys in a node and number of children for a node is depend on the order of the B-Tree. Every B-Tree has order.

B-Tree of Order m has the following properties...

• Property #1 - All the leaf nodes must be at same level.
• Property #2 - All nodes except root must have at least [m/2]-1 keys and maximum of m-1 keys.
• Property #3 - All non leaf nodes except root (i.e. all internal nodes) must have at least m/2 children.
• Property #4 - If the root node is a non leaf node, then it must have at least 2 children.
• Property #5 - A non leaf node with n-1 keys must have n number of children.
• Property #6 - All the key values within a node must be in Ascending Order.

For example, B-Tree of Order 4 contains maximum 3 key values in a node and maximum 4 children for a node.

Example

Operations on a B-Tree

The following operations are performed on a B-Tree...

1. Search
2. Insertion
3. Deletion

Search Operation in B-Tree

In a B-Ttree, the search operation is similar to that of Binary Search Tree. In a Binary search tree, the search process starts from the root node and every time we make a 2-way decision (we go to either left subtree or right subtree). In B-Tree also search process starts from the root node but every time we make n-way decision where n is the total number of children that node has. In a B-Ttree, the search operation is performed with O(log n) time complexity. The search operation is performed as follows...

• Step 1: Read the search element from the user
• Step 2: Compare, the search element with first key value of root node in the tree.
• Step 3: If both are matching, then display "Given node found!!!" and terminate the function
• Step 4: If both are not matching, then check whether search element is smaller or larger than that key value.
• Step 5: If search element is smaller, then continue the search process in left subtree.
• Step 6: If search element is larger, then compare with next key value in the same node and repeate step 3, 4, 5 and 6 until we found exact match or comparision completed with last key value in a leaf node.
• Step 7: If we completed with last key value in a leaf node, then display "Element is not found" and terminate the function.

Insertion Operation in B-Tree

In a B-Tree, the new element must be added only at leaf node. That means, always the new keyValue is attached to leaf node only. The insertion operation is performed as follows...

• Step 1: Check whether tree is Empty.
• Step 2: If tree is Empty, then create a new node with new key value and insert into the tree as a root node.
• Step 3: If tree is Not Empty, then find a leaf node to which the new key value cab be added using Binary Search Tree logic.
• Step 4: If that leaf node has an empty position, then add the new key value to that leaf node by maintaining ascending order of key value within the node.
• Step 5: If that leaf node is already full, then split that leaf node by sending middle value to its parent node. Repeat tha same until sending value is fixed into a node.
• Step 6: If the spilting is occuring to the root node, then the middle value becomes new root node for the tree and the height of the tree is increased by one.

Example

Construct a B-Tree of Order 3 by inserting numbers from 1 to 10.

Splay Tree

 Go to Animation

Splay tree is another varient of binary search tree. In a splay tree, the recently accessed element is placed at the root of the tree. A splay tree is defined as follows...

Splay Tree is a self - adjusted Binary Search Tree in which every operation on an element rearrange the tree so that the element is placed at the root position of the tree.

In a splay tree, every operation is performed at root of the tree. All the operations on a splay tree are involved with a common operation called "Splaying".

Splaying an element is the process of bringing it to the root position by performing suitable rotation operations.

In a splay tree, splaying an element rearrange all the elements in the tree so that splayed element is placed at root of the tree.

With the help of splaying an element we can bring most frequently used element closer to the root of the tree so that any operation on those element performed quickly. That means the splaying operation automatically brings more frequently used elements closer to the root of the tree.

Every operation on a splay tree performs the splaying operation. For example, the insertion operation first inserts the new element as it inserted into the binary search tree, after insertion the newly inserted element is splayed so that it is placed at root of the tree. The search operation in a splay tree is search the element using binary search process then splay the searched element so that it placed at the root of the tree.

In a splay tree, to splay any element we use the following rotation operations...

Rotations in Splay Tree

• 1. Zig Rotation
• 2. Zag Rotation
• 3. Zig - Zig Rotation
• 4. Zag - Zag Rotation
• 5. Zig - Zag Rotation
• 6. Zag - Zig Rotation

Example

Zig Rotation

The Zig Rotation in a splay tree is similar to the single right rotation in AVL Tree rotations. In zig rotation every node moves one position to thr righ from its current position. Consider the following example...

Zag Rotation

The Zag Rotation in a splay tree is similar to the single left rotation in AVL Tree rotations. In zag rotation every node moves one position to the left from its current position. Consider the following example...

Zig-Zig Rotation

The Zig-Zig Rotation in a splay tree is a double zig rotation. In zig-zig rotation every node moves two position to the right from its current position. Consider the following example...

Zag-Zag Rotation

The Zag-Zag Rotation in a splay tree is a double zag rotation. In zag-zag rotation every node moves two position to the left from its current position. Consider the following example...

Zig-Zag Rotation

The Zig-Zag Rotation in a splay tree is a sequence of zig rotation followed by zag rotation. In zig-zag rotation every node moves one position to the right followed by one position to the left from its current position. Consider the following example...

Zag-Zig Rotation

The Zag-Zig Rotation in a splay tree is a sequence of zag rotation followed by zig rotation. In zag-zig rotation every node moves one position to the left followed by one position to the right from its current position. Consider the following example...

---

Every Splay tree must be a binary search tree but it is need not to be balanced tree.

---

Insertion Operation in Splay Tree

The insertion operation in Splay tree is performed using following steps...

• Step 1: Check whether tree is Empty.
• Step 2: If tree is Empty then insert the newNode as Root node and exit from the operation.
• step 3: If tree is not Empty then insert the newNode as a leaf node using Binary Search tree insertion logic.
• Step 4: After insertion, Splay the newNode

Deletion Operation in Splay Tree

In a Splay Tree, the deletion operation is similar to deletion operation in Binary Search Tree. But before deleting the element first we need to splay that node then delete it from the root position then join the remaining tree.

AVL Tree

Download Animation 

AVL tree is a self balanced binary search tree. That means, an AVL tree is also a binary search tree but it is a balanced tree. A binary tree is said to be balanced, if the difference between the hieghts of left and right subtrees of every node in the tree is either -1, 0 or +1. In other words, a binary tree is said to be balanced if for every node, height of its children differ by at most one. In an AVL tree, every node maintains a extra information known as balance factor. The AVL tree was introduced in the year of 1962 by G.M. Adelson-Velsky and E.M. Landis.

An AVL tree is defined as follows...

An AVL tree is a balanced binary search tree. In an AVL tree, balance factor of every node is either -1, 0 or +1.

Balance factor of a node is the difference between the heights of left and right subtrees of that node. The balance factor of a node is calculated either height of left subtree - height of right subtree (OR) height of right subtree - height of left subtree. In the following explanation, we are calculating as follows...

Balance factor = heightOfLeftSubtree - heightOfRightSubtree

Example

The above tree is a binary search tree and every node is satisfying balance factor condition. So this tree is said to be an AVL tree.

---

Every AVL Tree is a binary search tree but all the Binary Search Trees need not to be AVL trees.

---

AVL Tree Rotations

In AVL tree, after performing every operation like insertion and deletion we need to check the balance factor of every node in the tree. If every node satisfies the balance factor condition then we conclude the operation otherwise we must make it balanced. We use rotation operations to make the tree balanced whenever the tree is becoming imbalanced due to any operation.

Rotation operations are used to make a tree balanced.

Rotation is the process of moving the nodes to either left or right to make tree balanced.

There are four rotations and they are classified into two types.

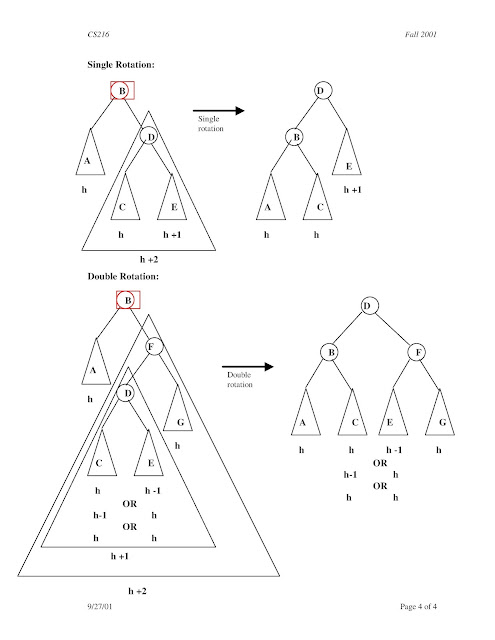
Single Left Rotation (LL Rotation)

In LL Rotation every node moves one position to left from the current position. To understand LL Rotation, let us consider following insertion operations into an AVL Tree...

Single Right Rotation (RR Rotation)

In RR Rotation every node moves one position to right from the current position. To understand RR Rotation, let us consider following insertion operations into an AVL Tree...

Left Right Rotation (LR Rotation)

The LR Rotation is combination of single left rotation followed by single right rotation. In LR Roration, first every node moves one position to left then one position to right from the current position. To understand LR Rotation, let us consider following insertion operations into an AVL Tree...

Right Left Rotation (RL Rotation)

The RL Rotation is combination of single right rotation followed by single left rotation. In RL Roration, first every node moves one position to right then one position to left from the current position. To understand RL Rotation, let us consider following insertion operations into an AVL Tree...

Operations on an AVL Tree

The following operations are performed on an AVL tree...

1. Search
2. Insertion
3. Deletion

Search Operation in AVL Tree

In an AVL tree, the search operation is performed with O(log n) time complexity. The search operation is performed similar to Binary search tree search operation. We use the following steps to search an element in AVL tree...

• Step 1: Read the search element from the user
• Step 2: Compare, the search element with the value of root node in the tree.
• Step 3: If both are matching, then display "Given node found!!!" and terminate the function
• Step 4: If both are not matching, then check whether search element is smaller or larger than that node value.
• Step 5: If search element is smaller, then continue the search process in left subtree.
• Step 6: If search element is larger, then continue the search process in right subtree.
• Step 7: Repeat the same until we found exact element or we completed with a leaf node
• Step 8: If we reach to the node with search value, then display "Element is found" and terminate the function.
• Step 9: If we reach to a leaf node and it is also not matching, then display "Element not found" and terminate the function.

Insertion Operation in AVL Tree

In an AVL tree, the insertion operation is performed with O(log n) time complexity. In AVL Tree, new node is always inserted as a leaf node. The insertion operation is performed as follows...

• Step 1: Insert the new element into the tree using Binary Search Tree insertion logic.
• Step 2: After insertion, check the Balance Factor of every node.
• Step 3: If the Balance Factor of every node is 0 or 1 or -1 then go for next operation.
• Step 4: If the Balance Factor of any node is other than 0 or 1 or -1 then tree is said to be imbalanced. Then perform the suitable Rotation to make it balanced. And go for next operation.

Example: Construct an AVL Tree by inserting numbers from 1 to 8.

Deletion Operation in AVL Tree

In an AVL Tree, the deletion operation is similar to deletion operation in BST. But after every deletion operation we need to check with the Balance Factor condition. If the tree is balanced after deletion then go for next operation otherwise perform the suitable rotation to make the tree Balanced.

 Example: Construct an AVL Tree

 

Binary Search Tree

In a binary tree, every node can have maximum of two children but there is no order of nodes based on their values. In binary tree, the elements are arranged as they arrive to the tree, from top to bottom and left to right.

A binary tree has the following time complexities.

1. Search Operation - O(n)
2. Insertion Operation - O(1)
3. Deletion Operation - O(n)

To enhance the performance of binary tree, we use special type of binary tree known as Binary Search Tree. Binary search tree mainly focus on the search operation in binary tree. Binary search tree can be defined as follows...

Binary Search Tree is a binary tree in which every node contains only smaller values in its left subtree and only larger values in its right subtree.

In a binary search tree, all the nodes in left subtree of any node contains smaller values and all the nodes in right subtree of that contains larger values as shown in following figure...

Example

The following tree is a Binary Search Tree. In this tree, left subtree of every node contains nodes with smaller values and right subtree of every node contains larger values.

---

Every Binary Search Tree is a binary tree but all the Binary Trees need not to be binary search trees.

---

Operations on a Binary Search Tree

The following operations are performed on a binary earch tree...

1. Search
2. Insertion
3. Deletion

Search Operation in BST

In a binary search tree, the search operation is performed with O(log n) time complexity. The search operation is performed as follows...

• Step 1: Read the search element from the user
• Step 2: Compare, the search element with the value of root node in the tree.
• Step 3: If both are matching, then display "Given node found!!!" and terminate the function
• Step 4: If both are not matching, then check whether search element is smaller or larger than that node value.
• Step 5: If search element is smaller, then continue the search process in left subtree.
• Step 6: If search element is larger, then continue the search process in right subtree.
• Step 7: Repeat the same until we found exact element or we completed with a leaf node
• Step 8: If we reach to the node with search value, then display "Element is found" and terminate the function.
• Step 9: If we reach to a leaf node and it is also not matching, then display "Element not found" and terminate the function.

Insertion Operation in BST

In a binary search tree, the insertion operation is performed with O(log n) time complexity. In binary search tree, new node is always inserted as a leaf node. The insertion operation is performed as follows...

• Step 1: Create a newNode with given value and set its left and right to NULL.
• Step 2: Check whether tree is Empty.
• Step 3: If the tree is Empty, then set set root to newNode.
• Step 4: If the tree is Not Empty, then check whether value of newNode is smaller or larger than the node (here it is root node).
• Step 5: If newNode is smaller than or equal to the node, then move to its left child. If newNode is larger than the node, then move to its right child.
• Step 6: Repeat the above step until we reach to a leaf node (e.i., reach to NULL).
• Step 7: After reaching a leaf node, then isert the newNode as left child if newNode is smaller or equal to that leaf else insert it as right child.

Deletion Operation in BST

In a binary search tree, the deletion operation is performed with O(log n) time complexity. Deleting a node from Binary search tree has follwing three cases...

• Case 1: Deleting a Leaf node (A node with no children)
• Case 2: Deleting a node with one child
• Case 3: Deleting a node with two children

Case 1: Deleting a leaf node

We use the following steps to delete a leaf node from BST...

• Step 1: Find the node to be deleted using search operation
• Step 2: Delete the node using free function (If it is a leaf) and terminate the function.

Case 2: Deleting a node with one child

We use the following steps to delete a node with one child from BST...

• Step 1: Find the node to be deleted using search operation
• Step 2: If it has only one child, then create a link between its parent and child nodes.
• Step 3: Delete the node using free function and terminate the function.

Case 3: Deleting a node with two children

We use the following steps to delete a node with two children from BST...

• Step 1: Find the node to be deleted using search operation
• Step 2: If it has two children, then find the largest node in its left subtree (OR) the smallest node in its right subtree.
• Step 3: Swap both deleting node and node which found in above step.
• Step 4: Then, check whether deleting node came to case 1 or case 2 else goto steps 2
• Step 5: If it comes to case 1, then delete using case 1 logic.
• Step 6: If it comes to case 2, then delete using case 2 logic.
• Step 7: Repeat the same process until node is deleted from the tree.

Example

Construct a Binary Search Tree by inserting the following sequence of numbers...

10,12,5,4,20,8,7,15 and 13

Above elements are inserted into a Binary Search Tree as follows...